На ЕГЭ по профильной математике проверяют, умеют ли школьники оперировать математическими понятиями, решать сложные задачи и, конечно, применять формулы. Мы собрали все формулы для ЕГЭ по математике в одной статье, чтобы облегчить вам подготовку к экзамену.
В этой статье:
Что будет в КИМ, а что нужно выучитьФормулы сокращенного умноженияАрифметическая и геометрическая прогрессииВероятностьСвойства степенейСвойства логарифмовТригонометрияПроизводныеПервообразные
Что будет в КИМ, а что нужно выучить
Для решения ЕГЭ по профильной математике школьникам предоставляют справочные материалы. Однако в них есть только четыре тригонометрические формулы:
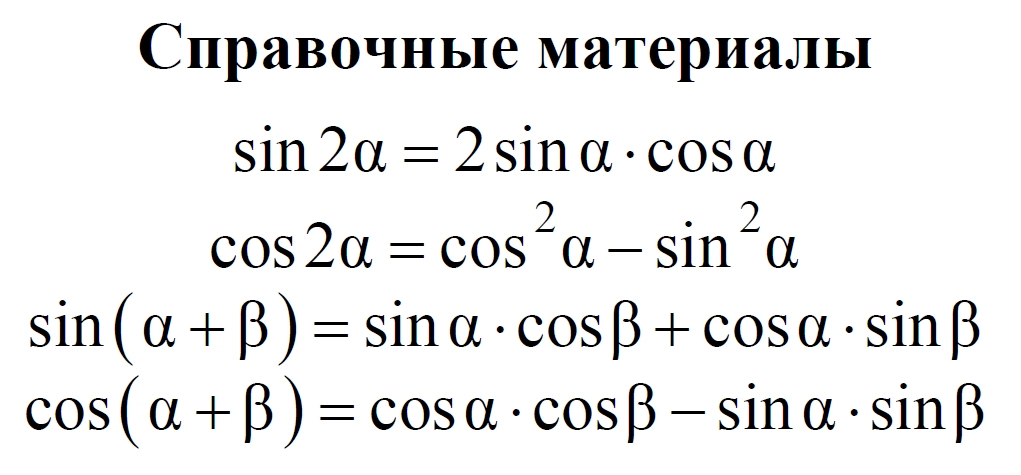
Информации по другим темам в справочных материалах нет, поэтому выход только один — выучить формулы. Но простая зубрежка в математике — плохой помощник. Чтобы запомнить основные формулы, нужно постоянно тренироваться и решать задания из ЕГЭ — тогда они точно отложатся в голове и на экзамене вспомнятся уже на автомате.
На курсах подготовки к ЕГЭ в MAXIMUM Education теорию объясняют простым языком, домашки дают в формате экзамена, а любой вопрос всегда можно задать преподавателю. С таким подходом высокий балл за ЕГЭ не будет проблемой!
Необходимые для выполнения ЕГЭ формулы можно разделить на несколько блоков. Рассмотрим каждый из них.
А на почте вас ждет полезный
подарок 😊 Скачать файл
Формулы сокращенного умножения
Формулы сокращенного умножения (ФСУ) изучаются еще в средней школе. Это один из самых часто применяемых способов решения в математике. ФСУ пригодятся при решении уравнений (задания 6, 13), неравенств (задача 15), преобразовании математических выражений (номера 7, 9), выполнении задания 18 на параметр, работе с функциями (задания 11, 12), а также при решении многих математических примеров для упрощения подсчетов.
Для успешной сдачи ЕГЭ по профильной математике необходимо запомнить следующие формулы.
Разность квадратов: a2 – b2 = (a – b)(a + b).
Квадрат суммы: (a + b)2 = a2 + 2ab + b2.
Квадрат разности: (a – b)2 = a2 – 2ab + b2.
Обратите внимание, что последние две формулы различаются только знаком перед 2ab: если вы ищете квадрат суммы, там стоит плюс, если квадрат разности — минус.
Квадрат суммы трех слагаемых: (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc.
Куб суммы: (a + b)3 = a3 + 3a2b + 3ab2 + b3.
Эта формула похожа на квадрат суммы, только а справа налево постепенно переходит от третьей степени до нуля, а b, наоборот, справа налево повышает свою степень — от нулевой до третьей. Перед a2b и ab2 вместо двойки стоит тройка.
Куб разности: (a – b)3 = a3 – 3a2b + 3ab2 – b3.
Если перед b стоял минус, там, где b будет в нечетной степени (первой и третьей), также будет минус.
Сумма кубов: a3 + b3 = (a + b)(a2 – ab + b2).
Разность кубов: a3 – b3 = (a – b)(a2 + ab + b2).
Всеми этими формулами можно пользоваться и в обратную сторону: если a2 – b2 = (a – b)(a + b), то и (a – b)(a +b) = a2 – b2.
Также a, b, c в формуле могут быть не только числом, но и отдельным математическим выражением, что иногда мешает старшеклассникам увидеть, где применяется ФСУ.
Арифметическая и геометрическая прогрессии
Эта тема встречается в задании 10 при решении текстовых задач, а также во второй части в номере 16.
Для арифметической прогрессии приняты следующие обозначения: a — член прогрессии, d — разность прогрессии (то есть число, на которое каждый последующий член увеличивается, если d положительно, или уменьшается, если d отрицательно), n — порядковый номер члена прогрессии.
Здесь пригодятся следующие формулы:
Разность прогрессии: d = an + 1 – an.
N-й член прогрессии: an = a1 + d(n – 1).
Также можно найти n-й член прогрессии как среднее арифметическое двух соседних членов:
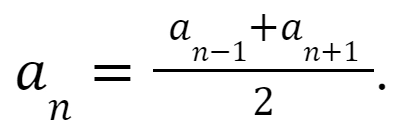
Сумма двух членов прогрессии: an + am = ap + aq, если n + m = p + q.
Сумма членов прогрессии:
- при известном последнем члене:
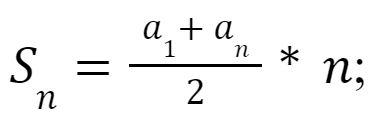
- при известной разности прогрессии:
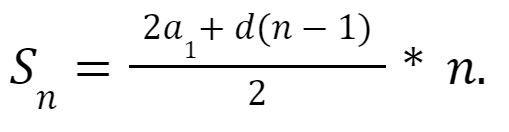
В случае с геометрической прогрессией член прогрессии обозначают как b, а число, во сколько раз увеличивается каждый последующий член или знаменатель прогрессии, как q.
N-й член прогрессии: bn = b1 * qn – 1.
N-й член прогрессии как среднее геометрическое двух соседних членов:
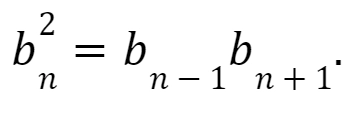
Произведение двух членов прогрессии: bn * bm = bp * bq при n + m = p + q.
Сумма членов прогрессии:
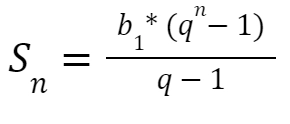
при q не равном 1.
Вероятность
В ЕГЭ по профильной математике встречается два задания на вероятность: номер 4 базового уровня сложности и 5 — повышенного.
Для работы с вероятностями нужно понимать определение вероятности: вероятность — это отношение числа благоприятных исходов к числу всех исходов.
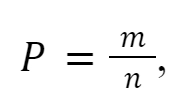
где P – искомая вероятность, m — число благоприятных исходов, n — число всех исходов.
Например, если мы побеждаем в настольной игре при выпадении числа 4 на игральном кубике, то число благоприятных исходов — 1 (победа только при выпадении одного числа), а число всех исходов — 6 (столько возможных чисел может выпасть). Тогда вероятность победы составляет 16.
Сумма вероятностей всех возможных событий составляет 1:
P1 + P2 + … + Pn = 1.
Чтобы найти вероятность двух взаимоисключающих событий, то есть вероятность того, что случится либо первое, либо второе событие, нужно сложить две вероятности:
P = P1 + P2.
Например, мы побеждаем в игре, если на кубике выпадает число 4 или 6. Чтобы найти вероятность победы, нужно сложить вероятности выпадения чисел 4 и 6:
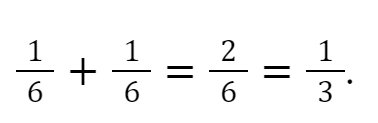
Если мы хотим найти вероятность двух не взаимоисключающих событий, то есть вероятность того, что оба события произойдут, нужно перемножить вероятности этих двух событий:
P = P1 * P2.
Например, мы бросаем кубик и побеждаем, если оба раза выпадает число 4. Значит, вероятность победы составляет
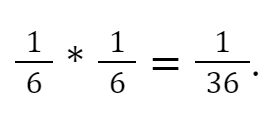
То есть, если мы ищем вероятность того, что произойдет ИЛИ первое, ИЛИ второе событие — складываем. Если ищем вероятность того, что произойдут ОБА события — умножаем.
Для решения заданий на вероятность необходимо знать всего четыре формулы, но все равно у старшеклассников возникают сложности с ними. Здесь нельзя слепо пользоваться формулами и просто делить меньшее число на большее. Важно логически рассмотреть условие задачи, при необходимости — сделать рисунок или схему.
Бесплатно
проверьте свой
уровень знаний
И скорректируйте подготовку к ОГЭ или ЕГЭ
Попробовать ООО «Юмакс», ИНН 7730681080, ERID 2VtzqwBLMVYСвойства степеней
Свойства логарифмов
Логарифмы могут встретиться на ЕГЭ по профильной математике как в первой части — в номерах 6, 7, 9, 11 и 12, так и во второй — в заданиях 13 (решение уравнений) и 18 (задание с параметром).
Логарифм — это действие, обратное возведению в степень. Если мы ищем b , то ищем степень, в которой число a даст число b.
Основные свойства логарифмов:
Тригонометрия
Тригонометрия встречается в заданиях 1, 2, 7, 9, 11–14 и 17. Рассмотрим формулы по заданиям.
Первая формула в тригонометрии дается школьникам довольно просто — это основное тригонометрическое тождество (ОТТ):
sin2x + cos2x = 1.
С этой формулой косвенно связана другая — произведение тангенса и котангенса:
tgx * ctgx = 1.
Дополнительно к ним в справочных материалах вы найдете еще четыре формулы, о которых мы рассказывали в начале статье:
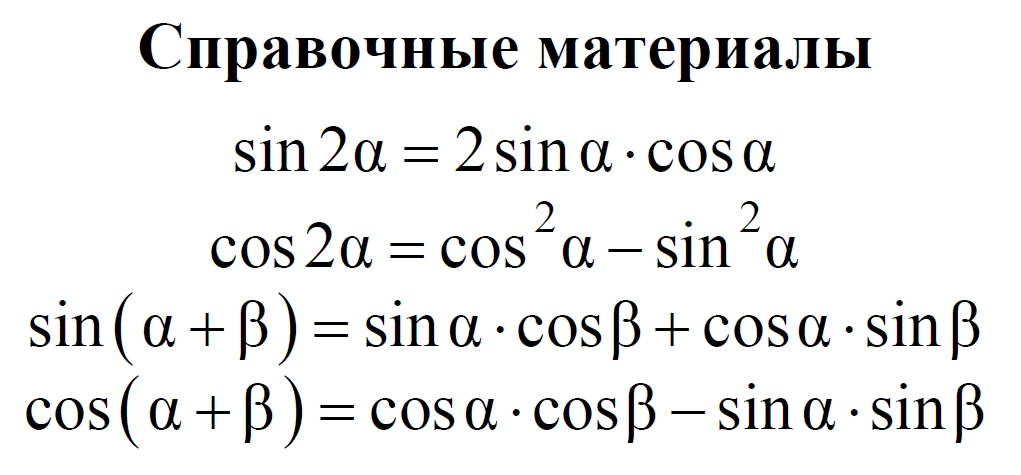
Кроме этих шести формул, для решения заданий, в которых встречается тригонометрия, старшеклассникам пригодятся еще несколько:
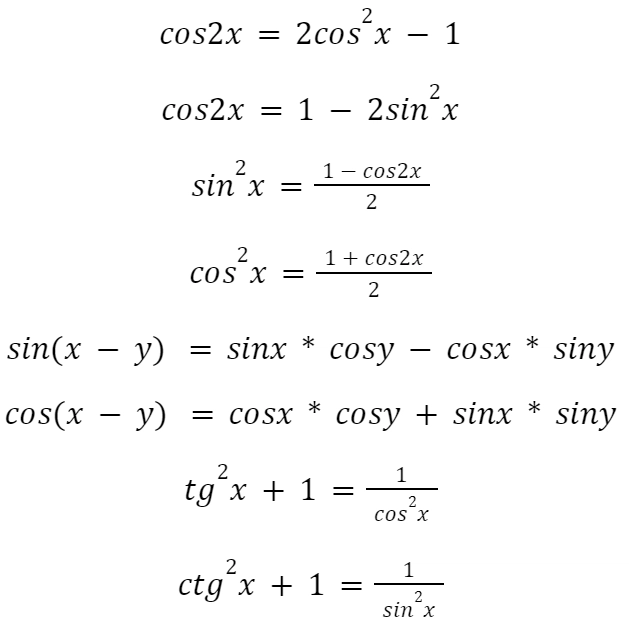
Заучить все тригонометрические формулы довольно сложно, поэтому обязательно научитесь выводить их. Как это сделать, используя ОТТ и справочные материалы, мы рассказали в этой статье.
Производные
Эта тема встречается в заданиях 8 и 12.
Производная — это скорость изменения функции. Если она положительна в данной точке, функция в этой точке возрастает, если отрицательна — убывает.
Если функция задана графиком, то производная в каждой точке графика отражает скорость изменения функции и численно равна тангенсу угла наклона касательной в этой конкретной точке к графику функции. Это геометрический смысл производной:
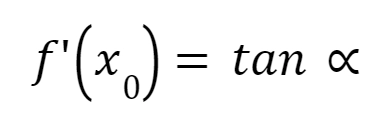
Если же функция задана формулой, то для ее нахождения воспользуйтесь правилами нахождения производной или правилами дифференцирования.
- Чтобы найти производную произведения функции на константу (число), нужно найти произведение этого числа и производной этой функции:
- Производная суммы (или разности) равна сумме (или разности) производных:
- Производную произведения двух функций можно найти по формуле
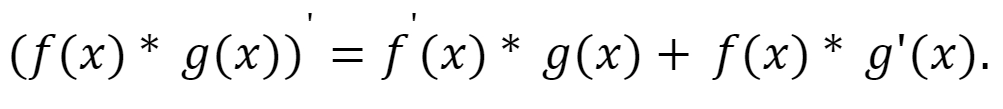
- Для нахождения производной частного двух функций необходима более сложная формула:
- Производная сложной функции равна произведению производной внешней функции на производную внутренней функции:
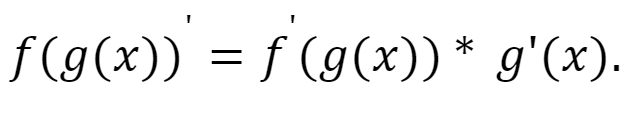
Значения производной для элементарных функций собраны в этой таблице:
Первообразные
Понятие первообразной функции пригодится в задании 8.
Функция F(x) является первообразной для функции f(x), если выполняется равенство F’(x) = f (x). То есть, если в предыдущей теме вы искали производную при известной функции, то здесь ищете функцию по известной производной. Поэтому функция F(x) и называется первообразной: она своеобразный «предок» функции f(x).
К сожалению, при нахождении первообразной нельзя просто воспользоваться таблицей для нахождения производной функции, приведенной выше. Если вы были внимательны, то заметили, что при нахождении производной функции f(x) = g(x) + С, где g(x) — любая функция, а С — некое число, мы в любом случае получаем производную функции g(x), а константа С теряется.
То есть для любой функции существует бесконечное число первообразных, ведь С может быть любым числом. Поэтому при нахождении первообразной нужно обязательно указывать +С, иначе мы не учитываем все возможные варианты первообразной.
Таблица для нахождения первообразной:
Нужные формулы для профильной математики не получится просто зазубрить: чтобы заработать на экзамене высокий балл, нужно понимать их и уметь применять в заданиях. Научиться делать это вы сможете на курсах подготовки к ЕГЭ в MAXIMUM Education. Опытный преподаватель, который сам написал экзамен на высокий балл, поможет вам разобраться в теории, научиться выводить нужные формулы и с их помощью решать задания без ошибок.
