Две трети выпускников проваливают 18 задание ЕГЭ по информатике. Как же его решать? Нужно знать особый подход. Давайте разберемся, как эффективно справиться с этим коварным заданием.
В этой статье:
Первая сложность в 18 задании ЕГЭ по информатикеВторая сложность в 18 задании ЕГЭ по информатикеКак упростить выражение? Что такое «красная зона»?Примеры 18 задания ЕГЭ по информатикеПодведем итогиВ ЕГЭ по информатике есть четыре задания на математическую логику. Сегодня речь пойдёт о задании №18, которое связано с анализом логического высказывания. Статистика ужасна: по оценке ФИПИ с ним справляются чуть меньше 1/3 сдающих. Почему 18 задание ЕГЭ по информатике вызывает сложности? Давайте разберемся, что надо знать, понимать и уметь, чтобы их избежать.
А если вас интересуют и другие задания, эффективно подготовиться к ЕГЭ по информатике можно на наших курсах.
Первая сложность в 18 задании ЕГЭ по информатике
Вам нужны знания не только математической логики, но и просто математики. В качестве логической переменной (которая может быть истина или ложна) выступают не просто некие x, y, z, а математические высказывания. В ответе надо определить значения некоторого параметра, зависящего от этих переменных. Что-то напоминает? Да, почти как в задании 18 из профильной математики, но тут будет намного проще. Например, логической переменной может выступать выражение «x>10» или суждение о том, что x кратен 5. Рассмотрим, как подходить к такому виду логической переменной.
Если логическая переменная — неравенство
Все просто. Выражение «x>10» истинно для всех х, которые являются решением данного неравенства, то есть для x от 10 до +∞. И это выражение ложно для всех x, которые можно описать неравенством (x≤10) или x∈(+∞; 10]. Обратите внимание на число 10, когда x=10, логическая переменная (x>10) ложна.
Если логическая переменная — утверждение
Допустим, наша переменная — «x делится на 5». Тогда она истинна для всех х, которые кратны 5 (0, 5, 10, 15,…). Обратите внимание на то, что 0 кратен любому числу, а значит кратен 5 и тоже даст истинное значение. Методом исключения, данная логическая переменная ложна при всех х, которые не делятся на 5.
Вторая сложность в 18 задании ЕГЭ по информатике
Когда такие переменные рассматриваются отдельно, все выглядит просто. Но в 18 задании у вас будет целое логическое высказывание, содержащее несколько переменных и параметр, значение которого вам надо определить.
Это и есть вторая сложность данного задания — надо знать, как правильно подходить к анализу выражения. Для этого нужно помнить о двух принципиальных шагах:
- Упрости, если есть возможность.
- Определи «красную зону»
18 задание ЕГЭ по информатике важно решать постепенно. Сначала поговорим об упрощении, так как без этого шага очень сложно начать анализ. Затем обсудим, что такое «красная зона».
Как упростить выражение?
Смысл этого шага в двух моментах:
- Введите обозначения для удобства записи. Иначе некоторые переменные получаются слишком громоздкими.
- Упростите зависимости логических переменных. Выражение, где смешаны несколько уровней скобок и логических функций, сложно анализировать. А вот идентичное ему выражение, в котором три переменных связаны дизъюнкцией, намного проще.
Для большинства заданий вам нужно знать несколько формул матлогики. Сохраните эту картинку, пригодится.

Что такое «красная зона»?
В задании нужно определить значения параметра, чтобы логическое высказывание было тождественно истинно при любых значениях переменной x. При этом мы не можем брать произвольно большой набор значений для искомого параметра, это также определяется условием задания. Поэтому нужно подбирать такие значения параметра, чтобы они закрывали только определённый ряд случаев, не больше и не меньше. Этот ряд случаев назовем «красной зоной», теми значениями переменной x, когда логическое высказывание не будет истинно при любых значениях параметра.
Простой пример. Возьмем логическое высказывание: (X < 50) V (X > A).
Нам не важно значение параметра А. У нас есть одно логическое слагаемое, которое истинно. Второе может быть ложно — дизъюнкция все равно в итоге даст истину. Значит «красная зона» — это все х≥50. Подбирать значение для параметра А необходимо только для случаев, когда х≥50, чтобы за счет второго слагаемого (где содержится А) обеспечить истинность всего выражения, когда первая скобка ложна.
Для правильного анализа красной зоны важно помнить об основных моментах анализа некоторых логических функций:
- Конъюнкция нескольких переменных будет истинна, только если каждый множитель истинен, и ложна, если хотя бы один множитель ложен.
- Дизъюнкция нескольких переменных будет истинна, если хотя бы одно слагаемое истинно, и ложна, только если ложны все слагаемые.
- Импликация ложна только в единственном случае — когда из истины следует ложь.
Примеры 18 задания ЕГЭ по информатике
Рассмотрим правильный подход на различных прототипах данного задания.
Пример 1
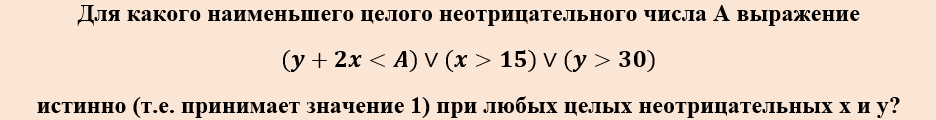
Решение
В данном логическом высказывании не требуется упрощений, так как у нас простой для анализа случай: дизъюнкция трёх переменных. Поэтому перейдём сразу к анализу и определению «красной зоны».
Вторая и третья скобки не зависят от А и обеспечат истинность всего выражения, независимо от параметра, если X>15 или Y>30. Тогда красной зоной будет ситуация, когда не выполняются ОБА из этих условий, то есть и вторая, и третья скобки одновременно ложны. Опишем этот случай системой:

В этой ситуации нам необходимо обеспечить истинность первой скобки, которая зависит от параметра. Дополним систему ещё одним условием.

Теперь мы свели задание к решению системы простейших неравенств. Определим границы для параметра А при помощи работы с неравенствами. Первое неравенство умножим на 2, затем сложим новое неравенство со вторым и сведём это всё к одному двойному неравенству за счёт одинакового выражения Y+2X.
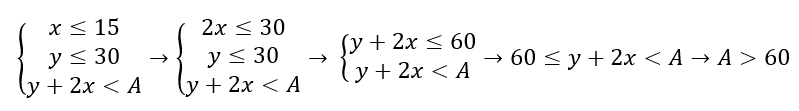
Осталось вернуться к формулировке вопроса. Вас всегда будут спрашивать что-то конкретное относительно значений параметра А! В данном случае нам надо найти наименьшее целое значение. В случае A > 60 наименьшим подходящим целым значением будет 61. Внимание! Всегда отслеживайте строгость и нестрогость знаков, значение 60 не подходит под условие A > 60, так как 60 равно 60, но не как не больше.
Ответ:
Пример 2

Здесь необходимо начать с упрощения выражения. Введём обозначения для краткости и удобства записи.
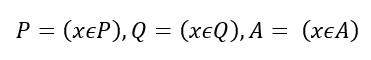
Выражение сразу выглядит намного проще.

Теперь применим формулу для раскрытия импликации на базовые функции.
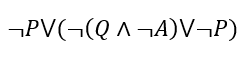
Далее воспользуемся формулой де Моргана.
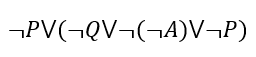
Уберём двойное отрицание и лишние скобки.
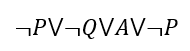
И финальным шагом уберём тавтологию.
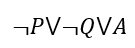
Сравните с тем, что было в условии. Стало проще, правда? Дальше мы будем анализировать именно это выражение.
«Красная зона» будет также определяться из случая, когда дизъюнкция будет истинна не из-за переменных, которые не зависят от А, а исключительно из-за переменной с параметром. Получается, для этого первое и второе слагаемые должны быть ложны. Получаем, что P = 1 и Q = 1, в таком случае и A = 1. Теперь вернёмся от наших обозначений к исходным описаниям переменных.
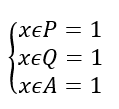
Значит наша «красная зона» — это пересечение отрезков P и Q. Чтобы покрыть ровно эту часть числовой прямой, отрезок А должен ровняться пересечению отрезков P и Q.
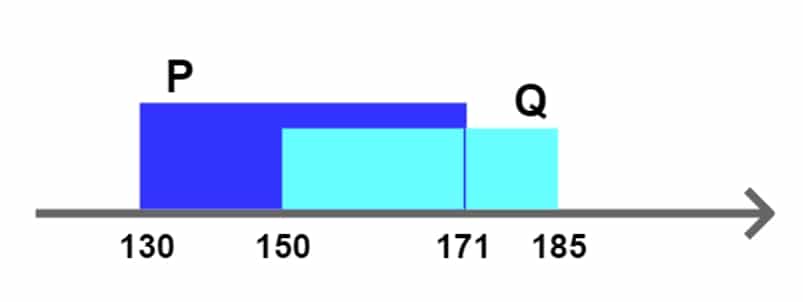
Получаем: A = [150; 171].
В ответ надо указать минимально возможную длину отрезка. Мы подбирали значение отрезка А так, чтобы сразу закрыть им только необходимое и не больше, поэтому полученный отрезок и есть отрезок минимальной длинны.
Длина отрезка считается очень просто: из большей границы вычитается меньшая. Длина отрезка А = 171 – 150 = 21.
Ответ: 21
Пример 3

Решение
В данном примере тоже нужно упростить выражение. Введём обозначения:
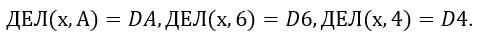
Получаем выражение
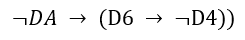
Дальше потребуется только раскрыть импликации, убрать двойное отрицание и лишние скобки.
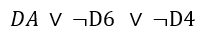
Теперь переходим к определению «красной зоны». Когда D6=1 и D4 = 1, то и DA должно быть истинно.
Вернемся к математическому смыслу наших переменных. Получаем условие: числа, которые кратны 4 и 6 одновременно, должны быть кратны и А. Пользуясь понятием наименьшего общего кратного (НОК) из математики, получаем, что числа, которые одновременно кратны 4 и 6 – это числа, кратные 12.
Переформулируем условие: числа, которые кратны 12, должны быть кратны А. Отсюда уже понятно, что А = 12. Если мы возьмём число меньшее, например 2, выражение будет истинно, но это не максимальное возможное значение, которое просят по условию. А если возьмём число больше, например 24, для x=12 выражение окажется ложным. Кратность 4 и 6 будет обнулять второе и третье слагаемое, а первое окажется ложно, так как 12 не кратно 24, а наоборот 24 кратно 12.
Ответ: 12
Пример 4

Решение
В этом примере встречается поразрядная конъюнкция. Суть этого вычислительного действия проста: мы выполняем логическое умножение чисел, записанных двоичным кодом, по разрядам (нулевой с нулевым, первый с первым и т.д.). Подробнее на поразрядную конъюнкцию взглянем уже при анализе выражения. Для начала упростим то, что надо анализировать. Введём обозначения:
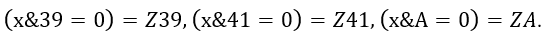
Получим выражение
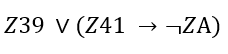
Дальше потребуется только раскрыть импликацию и убрать лишние скобки
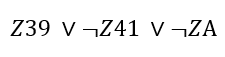
Теперь переходим к определению «красной зоны». Она возникает, когда Z39 = 0 и Z41 = 1, и ZA должно быть ложно.
Переходим обратно к математическому смыслу наших переменных. Запишем условия следующим образом: для х, для которых поразрядная конъюнкция с 41 даёт 0, а с 39 даёт не 0, поразрядная конъюнкция с А должна давать не 0.
Определим, что такое х из «красной зоны».
Посмотрим на первое условие: поразрядная конъюнкция с 41 даёт 0. Чтобы посчитать поразрядную конъюнкцию переводим 41 в двоичную систему счисления и получаем 1010012.
Чтобы в итоге поразрядной конъюнкции получился ноль, в тех разрядах, где в числе 41 стоят единицы, у числа х должны обязательно стоять нули. Там же, где в числе 41 стоят нули – в числе х может быть всё что угодно, так как одного нуля для обнуления произведения достаточно. Изобразим это схематически.
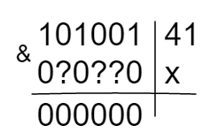
Мы получили некоторый «макет» чисел «красной зоны». Но он пока не полный. Переходим ко второму условию: поразрядная конъюнкция с 39 даёт не 0. Также необходимо перевести число в двоичную систему счисления. 3910 = 1001112. Чтобы в итоге поразрядной конъюнкции получить не 0, хотя бы один из разрядов, где у 39 стоят единицы, в х тоже должен содержать единицу. Достаточно одной, но она может быть на любом из доступных мест (кроме, тех, где из-за анализа первого условия мы уже поставили 0).
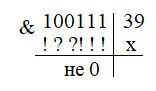
Теперь у нас есть полная схема чисел, которые представляют собой «красную зону». У таких чисел в нулевом, третьем, пятом разряде точно стоят нули, а в первом или во втором (или и в том и том) стоят единицы.
Теперь, чтобы определить наименьшее значение параметра А, при котором выражение будет тождественно истинно, надо обеспечить, чтобы при минимальном количестве единиц в разрядах (минимальном, но не меньше чем необходимо) можно было обеспечить ненулевое значение поразрядной конъюнкции иксов из «красной зоны» с числом А. Для этого нам обязательно надо закрыть единицами первый и второй разряды (тогда хотя бы в одном из этих разрядов точно получится 1), а остальные можно спокойно занять нулями.
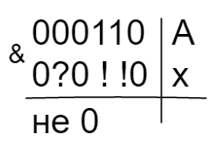
Последнее, что осталось сделать — перевести число А в десятичную систему счисления. 1102 = 610.
Ответ: 6
Подведем итоги
Теперь вы умеете решать 18 задание ЕГЭ по информатике. Такой подход с упрощением выражения и постепенным анализом позволяет разбить длительную работу с заданием на небольшие этапы. Вы постепенно составляете выводы о том, каким же должен быть параметр в этом задании.
Остается закрепить знания на практике. Напомню, что эффективно подготовиться к ЕГЭ по информатике можно на наших курсах. Используйте промокод BLOG0320 до 31 марта 2020 года включительно и получите первый месяц онлайн-подготовки со скидкой 50%.












Спасибо большое за статью.Все понятно и доходчиво.