Типичные ошибки ЕГЭ на профильной математике

Экзамен по профильной математике по праву считается одним из самых сложных для сдачи. За нескольких часов выпускникам нужно справиться с алгебраическими уравнениями, функциями, задачами по комбинаторике, геометрическими фигурами и процентами. Разбираемся, где школьники чаще всего теряются на экзамене и как не допустить типичных ошибок по математике, которые могут сильно повлиять на итоговый балл.

В этой статье:

Структура ЕГЭ по профильной математике Причины ошибок в ЕГЭ по профильной математике Типичные ошибки на ЕГЭ по математике Разбор заданий, в которых чаще всего ошибаются

ЕГЭ по профильной математике — экзамен для отважных школьников, которые уверены в своих знаниях и собираются поступать на сложную специальность. Не переживать о подготовке и итоговом балле вам помогут курсы по ЕГЭ в MAXIMUM Education. Заручитесь поддержкой опытного преподавателя, чтобы показать на экзамене класс!

Структура ЕГЭ по профильной математике

На ЕГЭ по профильной математике отводится 3 часа 55 минут. Экзамен состоит из двух частей и 19 заданий, в сумме дающих 32 первичных балла. Все номера делятся на три блока:

«Алгебра и начала математического анализа» — 12 заданий, 21 первичный балл;
«Вероятность и статистика» — 2 задания, 2 первичных балла;
«Геометрия» — 5 заданий, 9 первичных баллов.

Первая часть экзамена включает 12 заданий с кратким ответом в виде целого числа или конечной десятичной дроби. За каждый номер можно получить один первичный балл, всего — 12, это 37,5% от всей работы. Ответы записываются в специальный расчерченный бланк, где на каждый знак, в том числе запятую или минус, дается отдельная клетка.

Вторая часть состоит из 7 заданий с развернутым ответом — 5 по алгебре и 2 по геометрии:

№ 13 — рациональные, тригонометрические, логарифмические уравнения и их системы, 2 балла;
№ 14 — стереометрическая задача, 3 балла;
№ 15 — неравенства, 2 балла;
№ 16 — финансовая задача, 2 балла;
№ 17 — планиметрическая задача, 3 балла;
№ 18 — задача с параметром, 4 балла;
№ 19 — работа с числами и их последовательностями, 4 балла.

В 2024 году в первой части появилось новое задание по теме «Векторы». Стоить оно будет так же, как и остальные вопросы этой части, — 1 балл.

Структура ЕГЭ по всем предметам, в том числе по математике, количество заданий и темы, которые встретятся в КИМ, определены в специальном документе — кодификаторе. Он размещен на сайте ФИПИ — составителей экзамена. Что полезного можно узнать из этого документа, читайте в нашем гайде.

Причины ошибок в ЕГЭ по профильной математике

Невнимательность

К сожалению, врагом на экзамене становится тот, от которого не ждешь подвоха, — глаза. Ребята, разнервничавшись, часто видят не те числа и степени, переписывают в черновик другое уравнение и подолгу бьются над задачей, которую придумали не составители, а они сами.

В результате теряется драгоценное время и баллы. При решении всех заданий необходимо несколько раз сверяться с условием, потому что самая обидная ошибка — верно решить задание, которого не было.

Вычисления

При подготовке к экзамену многие школьники, стараясь сэкономить время, пользуются калькулятором. Но машинные подсчеты приносят больше вреда, чем пользы, потому что на экзамене приходится считать вручную. Если вы к этому не привыкли, можете быстро устать от больших чисел и ошибиться в подсчетах в столбик, которыми уверенно пользуются пятиклассники.

Согласитесь, обидно потерять балл не за незнание математики, а за неправильно возведенное в степень число? Совет — отложите калькулятор и не пользуйтесь им ни на уроках математики, ни при самостоятельной подготовке, чтобы ваша голова привыкла к большим числам и щелкала их как орешки.

Незнание формул

Этот пункт касается и алгебры, и геометрии. Необходимо выучить на зубок все формулы сокращенного умножения, формулы приведения в тригонометрии и геометрические формулы, чтобы не ломать голову — где возвести в куб, а где умножить на четыре?

Неудобный чертеж

Многие ребята, решая 14-е задание блока «Стереометрия», останавливаются еще на этапе чертежа, потому что их рисунок вызывает больше вопросов, чем ответов. Чертеж может быть построен верно, но, глядя на него, запутываешься еще больше. Залог успеха в стереометрических задачах — чертежи с разных ракурсов. Так вы сможете разглядеть все детали, и ни одна точка, прямая или квадрат не потеряются.

Физическое и эмоциональное состояние

Экзамен — причина большого стресса для школьников. Даже круглый отличник, нервничая, ошибается в тех заданиях, которые он бы с легкостью решил бы в другой обстановке.

Поэтому в период ЕГЭ нужно постараться свести стресс к минимуму. Перед экзаменом стоит выспаться, позавтракать, обязательно взять с собой воду, шоколадку и хороший психологический настрой. К экзамену стоит относиться как к жизненному этапу, который пройдет позитивно и быстро.

Типичные ошибки на ЕГЭ по математике

Путаница в определениях

Частая ошибка в ЕГЭ по профильной математике — незнание определений. В заданиях на арифметическую прогрессию выпускники путают сумму всех членов прогрессии и начальный член, подставляя не те числа в исходно верную формулу и получая неверные ответы.

В геометрических задачах старшеклассники путают медиану, биссектрису и высоту, катет и гипотенузу, поэтому ищут совсем не то, что нужно. Чтобы избежать таких ошибок, перед экзаменом стоит повторить все основные термины и определения, даже если они кажутся совсем простыми.

Потерянный минус

Часто школьники при переносе числа из одной части уравнения в другую забывают поменять знак. После этого этот потерянный минус ломает всё решение: даже если потом ошибок допущено не будет, ответ всё равно выйдет неверный. Именно поэтому нужно взять в привычку после каждого преобразования в уравнении проверять: а не потерялся ли минус?

Неизмененный знак в неравенстве

Когда в школе только начинают проходить неравенства, все узнают, что при умножении всего неравенства на отрицательное число знак неравенства меняется на противоположный. Но, к сожалению, спустя несколько лет на ЕГЭ многие выпускники забывают поменять этот знак. Эта ошибка, как и потерянный минус в уравнении, автоматически губит все последующие шаги.

Значения тригонометрических величин

Ребята часто забывают, чему равен синус 60 градусов или косинус от 𝝅 / 6, из-за чего допускают ошибки в решении тригонометрических уравнений. Некоторые вещи нужно просто выучить — и это одна из них.

Отсутствие проверки корней по ОДЗ

Большинство старшеклассников помнит: первое, что необходимо сделать при решении уравнения, — определить область допустимых значений (ОДЗ). Но гораздо меньше помнит еще кое-что: когда вы заканчиваете решать уравнение и находите корни, их необходимо сверить с ОДЗ. Часто в ответ записывают корни, которые на самом деле решением уравнения не являются.

Некорректное оформление

Во второй части ЕГЭ по профильной математике ребята часто не записывают в бланк те шаги, которые кажутся им очевидными. Например, последовательные преобразования в алгебраических уравнениях или этапы доказательства в геометрических задачах.

Нужно помнить, что во второй части вы получаете баллы не столько за ответ, сколько за каждый шаг в решении. Поэтому стоит записывать свои мысли как можно более подробно, чтобы ни один балл не потерялся.

Разбор заданий, в которых чаще всего ошибаются

Давайте проведем анализ типичных ошибок по математике, которые выпускники допустили на ЕГЭ в прошлом году.

Задание 1: планиметрия

В этом задании чаще всего ошибались, посчитав, что средняя линия, проведенная в треугольнике, делит его на фигуры равной площади. Это не так! На самом деле площади треугольника и трапеции, образовавшихся при проведении средней линии, соотносятся как 1 : 4. То есть площадь треугольника будет в 4 раза меньше площади трапеции.

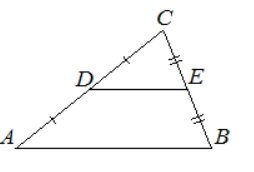
Условие. Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Решение. Так как DE — средняя линия, треугольники ABC и CDE — подобны. Причем коэффициент подобия для них составляет 2, то есть все стороны треугольника ABC в 2 раза больше, чем стороны треугольника CDE. То же самое касается медианы, биссектрисы и высоты, проведенной в этих треугольниках. Высота, проведенная в треугольнике ABC, будет в 2 раза больше высоты, проведенной в CDE.

Площадь треугольника можно найти по формуле

где h — высота, проведенная в треугольнике, а a — сторона, к которой эту высоту провели.

Таким образом, если площадь треугольника CDE составляет

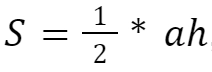
а высота и сторона, к которой провели эту высоту, в треугольнике ABC в 2 раза больше, чем высота и сторона в треугольнике CDE, то площадь треугольника АВС составляет

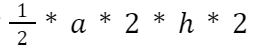
или

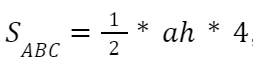
то есть в 4 раза больше площади CDE. Если площадь АВС составляет 24, тогда площадь CDE в 4 раза меньше, то есть 6.

Теперь остается найти только площадь трапеции. Площадь треугольника АВС — это сумма площадей CDE и трапеции. Значит, площадь трапеции составляет 24 – 6 = 18.

Ответ: 18.

Задание 3: стереометрия

В этом задании ЕГЭ ребята часто допускают ошибки, неверно учитывая масштаб. Например, многие посчитали, что при увеличении радиуса основания конуса в 2 раза, площадь его основания также увеличивается вдвое. Но, согласно формуле площади круга

при увеличении радиуса в 2 раза площадь увеличивается в 4 раза. Чтобы избежать ошибок в подобных заданиях, всегда стоит записывать формулы в черновик и затем вносить в них изменения: какое число умножили на 2, какое разделили на 8 и так далее.

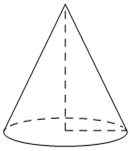
Условие. Во сколько раз увеличится объем конуса, если радиус его основания увеличится в 11 раз, а высота останется прежней?

Объем конуса рассчитывается по формуле

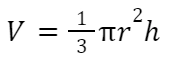
где r — радиус основания, а h — высота конуса. Если объем исходного конуса составлял

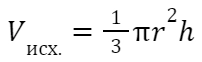
радиус основания увеличился в 11 раз, а высота не изменилась, то объем нового конуса составит

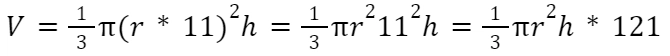
то есть в 121 раз больше, чем объем исходного конуса.

Ответ: 121.

Задание 5: вероятность события

В этом задании многие выпускники потеряли баллы, так как привыкли пользоваться заученными формулами и правилами, а не анализировать условие. Часто ребята, решая задания с вероятностями, привыкли просто находить большее и меньшее число в условии и делить меньшее на большее. Вуаля! Получается дробь, которая затем идет в ответ. Признавайтесь, делали так хоть раз? Но решать таким методом не стоит хотя бы потому, что в ЕГЭ по профильной математике подобные задачи часто решаются не в один шаг.

Условие. У Маши в кармане было 2 монеты по 2 рубля и 4 монеты по 5 рублей. Маша, не глядя, переложила 3 монеты в другой карман. Найдите вероятность того, что двухрублевые монеты лежат теперь в одном кармане.

Решение. Как бы нам ни хотелось разделить 2 на 6, сделать так не получится. Тогда мы получим бесконечную десятичную дробь, которую не сможем записать в бланк ответа. Что же делать?

Давайте проанализируем условие и представим его несколько иначе: пусть Маша вместо того, чтобы перекладывать монеты туда-сюда, сначала положит их все на стол. Затем она положит одну двухрублевую монету в случайный карман. Мы помним, что по итогу у Маши в каждом кармане должно оказаться по 3 монеты.

Значит, в одном кармане, где уже оказалась двухрублевая монета, остается еще 2 свободных «места», на которые может попасть вторая двухрублевая монета. В другом кармане, который еще пуст, таких свободных мест 3, ведь в кармане должно оказаться 3 монеты. Значит, вторая двухрублевая монета может занять любое место из этих 5. Тогда вероятность того, что две двухрублевые монеты попадут в один карман, составляет

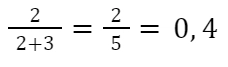
Ответ: 0,4.

Задание 8: производная

Здесь ошибки у старшеклассников возникают из-за непонимания смысла производной. Многие считают, что если функция в какой-либо точке отрицательна, то и производная тоже, и наоборот. На самом деле это совсем не так.

Производная — это математическое отражение пути функции. Например, если функция «поднимается» (возрастает), то ее производная положительна, если «падает» (убывает), то производная отрицательна. Так как в одной точке графика функция может возрастать, а другой убывать, то и производная в разных точках функции будет разной. Поэтому знак производной не зависит от знака функции. Например, функция в точке x может быть отрицательной, но при этом возрастать — поэтому производная ее в данной точке будет положительна.

Кроме того, на графике видно, что иногда функция возрастает совсем медленно, а иногда буквально «взлетает». Получается, что скорость возрастания функции будет в этих точках разной, значит, и производная будет отличаться.

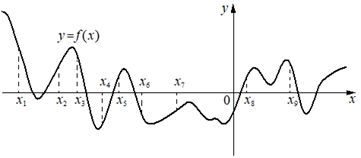
Условие. На рисунке изображен график функции y = f(x). На оси абсцисс отмечено девять точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉. Найдите количество отмеченных точек, в которых производная функции f(x) отрицательна.

Решение. Если нам нужно найти точки, в которых производная отрицательна, значит, мы будем искать те, в которых функция убывает. На графике видно, что функция убывает в точках x₁, x₃, x₆, x₉. Значит, нам подходит 4 точки.

Ответ: 4.

Так же легко справляться с задачами и не допускать ошибок на ЕГЭ по математике-профилю вы научитесь на курсах подготовки в MAXIMUM Education. Вся необходимая теория на онлайн-платформе, отработка экзаменационных заданий, лайфхаки и советы опытного преподавателя — всё это ждет вас на занятиях. Места в группах еще есть!

Типичные ошибки в ЕГЭ по профильной математике, о которых нужно знать

Структура ЕГЭ по профильной математике

Как подготовиться к ОГЭ на отлично?